미래 기후 환경에서 꿀벌응애 개체군 동태 모의연구

서 론

꿀벌응애(Varroa spp.)는 1904년 인도네시아 자바섬에서 동양종꿀벌(Apis cerana)에 외부기생하는 것으로 Varroa jacobsoni Oudemans가 보고되었다. 그 후 서양종꿀벌(Apis mellifera L)이 아시아권으로 도입되면서 기주전환(Host switch)이 이루어져, 1951년 싱가포르, 1960년대에는 홍콩, 필리핀 등지에서 서양종꿀벌에 기생하고 있음이 확인된 이후 세계적으로 확산되어, 현재 꿀벌응애는 꿀벌 건강의 가장 큰 위해 요소로 자리잡고 있다(Peng et al., 1987; Oldroyd, 1999). 분자생물학의 발달에 힘입어 전세계 분포 꿀벌응애의 유전형 분석 결과, 아시아 대륙에 분포하는 개체군은 아시아 태평양 도서지역종인 V. jacobsoni와는 다른 V. destructor로 구분 명명하였다(Anderson and Trueman, 2000). 국내에는 1950년 마산에서 보았다는 증언이 있으며, 1968년에는 전국적으로 확산되었고, 피해는 점차 심해지는 것으로 보고되었다(최 등, 1986; 우 등, 1994; 정 등, 2000). 꿀벌응애 개체군 밀도는 7~8월에 가장 높아지고, 이로 인한 꿀벌 개체수의 감소폭도 약 30~50% 정도로 추정하고 있다(최 등, 1986; 우와 이, 1993; 우 등, 1994; 이 등, 2004).

Jung and Kim(2008)은 7월 이후 2개월간 꿀벌응애 개체군 증가 유형을 바탕으로 지수함수 모형을 적용시켜, 개체군 증가율은 0.08에 이르고, 방제수준은 꿀벌 기생율이 10%가 넘지 않아야 한다고 제시하였다. 이후 꿀벌응애의 생활사에 기반한 process 모형이 개발되었다. 꿀벌응애 암컷 성충은 꿀벌의 외부에 편승하고 있다가(편승기간: phoretic phase) 봉개 직전의 유충방으로 침입한다. 침입 후 소방의 바닥으로 내려갔다가 봉개된 이후 번데기로 발육하는 유충의 혈림프를 섭취하고 산란을 시작한다(산란기간, reproductive phase). 첫 산란은 반수체 수컷이 되고, 그 다음부터는 배수체 암컷이 된다. 대개 산란 간격은 약 30시간이다. 성충이 된 응애는 소방 안에서 교미하고 그 중 교미한 암컷만이 출방하는 꿀벌에 기생하여 소방을 빠져나오고, 탈출하지 못한 수컷이나 미발육 암컷들은 대게 죽게 된다(Martin, 1995b, 1998). 각 행동 단계별로 수학적 함수를 구성한 후, 전체의 조각을 엮으면 전체 개체군 변동을 모의할 수 있다(Martin, 1998; Calis et al., 1999). Jung(2009)은 Martin(1998)과 Wilkinson and Smith(2002)이 개발한 수리모형을 국내 봉군 환경에 적응시킨 한국형 꿀벌응애 개체군 동태 모형을 개발하였다. Jung(2009)은 모형 시뮬레이션을 통해 국내 봉군에서 꿀벌응애의 개체군의 증가율은 봄철 육아가 왕성할 때에는 0.04 내외로 유지되고, 늦여름 육아가 중단된 이후에는 0.01에서 0.003으로 떨어질 수 있음을 보였고, 이를 통해 산란 억제 등의 방법이 꿀벌응애 개체군 밀도 조절에 영향을 줄 수 있음을 증명했다. Jung(2012)은 이 모형에서 꿀벌응애의 밀도와 꿀벌개체군 밀도간의 연결함수가 없음을 확인하고, 피해함수(damage function) 삽입을 통해 꿀벌응애 밀도가 증가함에 따라 임계밀도에서 꿀벌 개체군은 폐사하고 이에 따라 지역적으로 꿀벌응애 개체군도 사멸할 수 있음을 증명하였다. 그 결과 여름철의 분봉(hive spliting)은 꿀벌응애의 생식 공간인 육아방 제거의 효과로 나타나기 때문에 꿀벌응애 밀도 억제에 큰 영향을 준다고 보고하였다.

비록 2006년 이후 붉어진 봉군절멸현상(Colony Collapse Disorder: CCD)에 대한 핵심적 인과관계는 밝혀지지 않았다. 봉군절멸현상과 이스라엘급성마비바이러스(IAPV) 유무와 아주 높은 상관관계를 보이며, 그 바이러스 발병과 꿀벌응애의 기생여부도 밀접한 관계를 가진다(최 등, 2007; Cox and van Engelsdorf, 2009). 그럼에도 불구하고 봉군절멸현상은 꿀벌의 내외부 기생성 병해충, 질병, 화학약제의 남용, 환경 스트레스, 꿀벌의 사료 주입 및 영양 결핍, 장거리 꿀벌집단의 이동, 무분별한 봉군 또는 여왕벌의 수입, 그리고 최근 일련의 기후변화 등 다양한 요인이 복합적으로 작용한 스트레스 현상으로 인식되고 있다(Watanabe, 2008; Cox and van Engelsdorf, 2009). 특히 2000년대 이후의 기후변화 패턴(양상)은 꿀벌 건강을 더욱 위협할 뿐 아니라 꿀벌-기생성 응애류의 상호작용에도 영향을 미칠 수 있다. 특히 한반도는 기후변화의 핫스팟(Hot spot)으로, 1906년부터 2005년까지 관측된 전 지구 지표면 평균온도는 0.7°C 증가하였고, 육지 온도는 0.9°C 증가하였는데(IPCC, 2007), 한반도의 온도는 그 2배 이상인 1.7°C 증가하였다(기상청, 2012). 앞으로 기후는 예전에 비해 겨울이 늦게 온다. 겨울철 온도가 높아지고, 봄이 빨리오며, 여름철 폭염기간이 늘어남과 동시에 여름철 이상기후일수가 증가할 것으로 예측하였으며, 이에 따라 다양한 생물의 적응 현상이 예측된다. 특히 곤충은 크기가 작은 외온성 동물이기에 외부 온도 환경 변화에 영향이 더 크며, 생활사가 짧고 번식력이 강하며 분산이동 능력이 큰 특징을 가지고 있다. 따라서 기후 변화에 대한 반응은 크게 생물계절패턴의 변화(phenology), 분포 지역의 변화(distributional shift), 그리고 타 환경과의 상호관계의 변화(Interaction) 등으로 나타날 수 있다(Andrew et al., 2013). 특히 꿀벌은 대규모 집단을 이루어 사회성 생활을 하는 곤충으로, 기후 변화의 영향은 더 클 것으로 예측되었으며, 외부 기생성 응애류와의 상호작용 양상도 달라질 것으로 전망하였다(Le Conte et al., 2010). 본 연구는 Jung(2012)에서 개발된 꿀벌응애 개체군 모형을 활용하여, 미래 기후 환경에서 꿀벌응애 개체군 변동을 모의하고, 꿀벌응애 관리를 위한 전략을 개발하기 위해 수행되었다.

재료 및 방법

미래 기후 환경

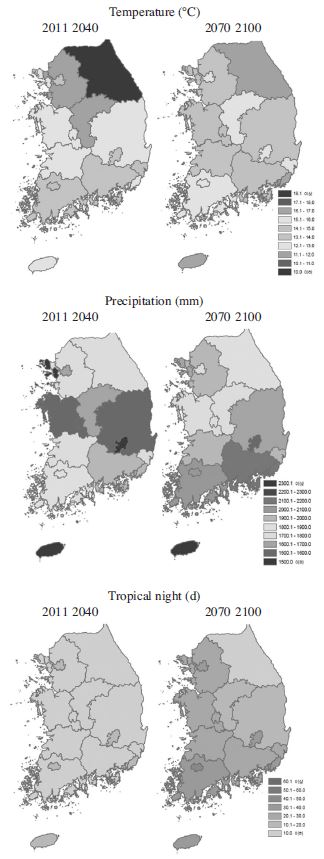
미래 기후 환경은 RCP4.5 시나리오를 기반으로 기상청(2012) 자료를 바탕으로 구성하였다(Table 1). 폭염(Heat wave)은 일최고온도가 33°C 이상인 날로써 열파 발생에 따른 보건, 대기환경 및 주간 에너지 사용량 등과도 관련이 깊다. 통상 폭염주의보는 폭염이 2일간 지속될 경우를 발령한다. 열대야(Tropical night)는 일몰 후 일출 전까지 기온이 25°C 이하로 내려가지 않는 날을 말하며, 여름일수(Summer day)는 일최고기온이 25°C 이상이 되는 연간일수로 정한다. 식물성장기간(Plant growth duration)l은 일평균기온이 5°C 이상 6일간 지속된 첫날부터 시작되며 일평균기온이 5°C 미만으로 6일 이상 지속된 첫날까지의 합계일로 규정된다. 겨울철 기후와 관련된 서리일수(frost day)는 일최저기온이 0°C 미만인 날의 연중 일수이며, 결빙일수(Ice day)는 일최고기온이 0°C 미만인 날의 연중일수를 말한다. 호우일수(heavy rain day)는 일강수량이 80mm 이상인 날의 연중일수이다(기상청, 2012). 현재 기후값은 2001년부터 2010년까지 전국 광역지자체별 평균값 중 최저값과 최고값을 취했으며, 미래기후값은 2011~2040년의 평균값과 2017~2100년 평균 값을 취했다. Fig. 1에는 두 기간의 추정치를 그림으로 제시하여 그 경향을 파악할 수 있게 하였으며, Table 1에는 후자의 추정치만을 제시하였다. 또한 Table 1에 현재값과 미래추정치 사이의 변동양상을 백분율로 나타냈다.

Table 1.

Projected future climate conditions compared with current climate (Data extracted from KMA, 2012) and its possible impact on honeybee

Fig. 1.

Projected climate change in Korean peninsula based on RCP4.5 scenario. Figure was modified from KMA, 2012.

꿀벌응애 개체군 모형

꿀벌응애 생활사에 대한 주요 부모형은 편승기간, 소방침입기 그리고 번식기간으로 나누어 각각을 정량화 가능 단위로 나누었다(Fig. 2). 편승기간의 주요인은 일벌의 수, 자연낙마율 등의 꿀벌응애 사망요인, 침입기에는 유충 소방수와 일벌의 청소행동, 번식기에는 산란, 발육, 교미를 다 마칠 수 있는 시간과 자원 등이 중요하다(Wilkinson and Smith, 2002; Jung, 2009, 2012).

Fig. 2.

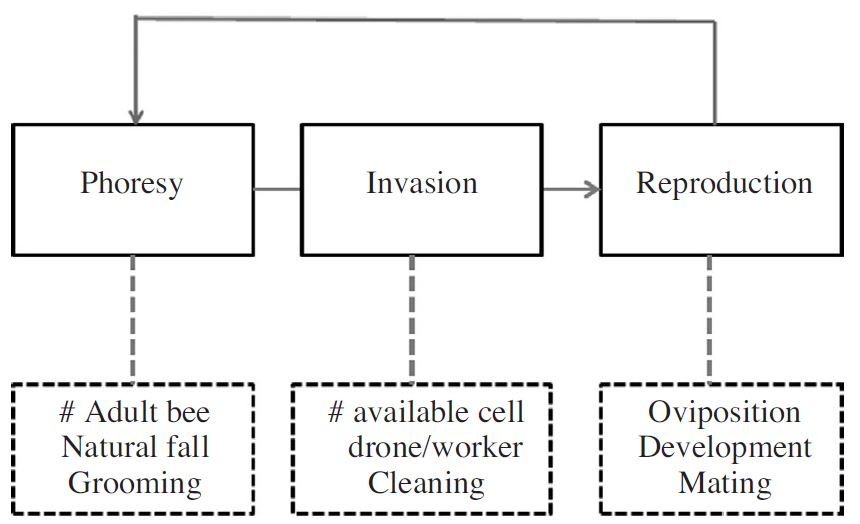
Major components of Varroa population model relative to its life cycle (solid line) and factors on each element (dotted line).

Table 2.

Mathematical representation of the major components of the submodels including the damage function

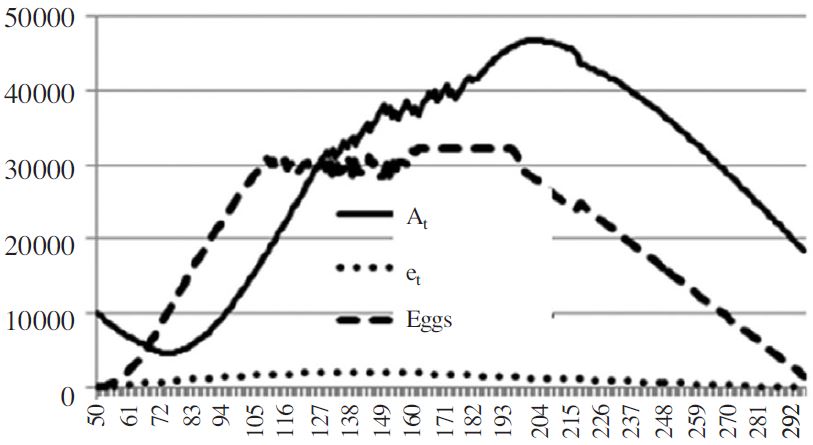
꿀벌응애 개체군 크기는 꿀벌 성충에 편승하고 애벌레방에서 번식하기 때문에 꿀벌 일벌 성충과 애벌레 방에 대한 각각의 정보가 필요하다. 또한 꿀벌응애의 편승 및 애벌레 감염을 통해 꿀벌응애의 밀도는 증가할 수 있지만, 임계밀도(10%) 이상이 되었을 때는 꿀벌 개체군 증가에 부정적 영향을 미친다. 이를 피해함수의 형태로 적용시킨다(Table 2, Jung, 2012). 꿀벌 일벌의 개체수(A_t+1))는 당일 벌의 수(A_t))에 21일 전 산란수(e_t-21)를 더하고 당일 일벌 사망수(A_tQ_t)를 제하면 된다(Table 2). 일벌 사망률은 여름철 꿀벌 수명을 30일, 겨울철 100일로 가정하여 계산하였다(Neukirch, 1982). 여왕의 산란수는 최대산란수(μ=2000)에 일일 산란수 분포(S_t)를 곱하는 것으로 구할 수 있다. 산란수 분포는 sin 함수를 이용하여, 년 2주기의 산란분포를 가정하고, 가을철 산란은 편의상 봄철의 0.5배로 하였다. 꿀벌응애는 산란 후 8일이 된 일벌방에 침입하므로, 꿀벌응애가 침입 가능한 일벌 애벌레 방의 수(W_t)는 e_t-8이 된다. 침입 가능한 수벌 애벌레 방의 수(D_t)는 편의상 일벌방의 일정 퍼센트(4%, Wilkinson and Smith, 2002)로 고정하였다 (Jung, 2009, 2012).

꿀벌에 편승하는 꿀벌응애 수(P)는 현재 편승 꿀벌응애의 수에 새로 출방하는 꿀벌에 기생하여 소방에서 탈출하는 꿀벌응애 수(E)를 더하고, 새로이 소방으로 침입하는 꿀벌응애의 수(I)와 당일 사망(주로 꿀벌에서 떨어지거나 꿀벌이 뜯어 냄)한 꿀벌응애의 수(G)를 제한다. 출방하는 벌과 함께 소방에서 나오는 꿀벌응애의 수(E)는 출방 12일(일벌) 또는 14일(수벌) 전에 소방으로 침입한 암컷 응애의 수에 그 암컷이 생산한 암컷 성충 응애 수를 합하고(I_t-12+R_t-12), 출방하는 응애의 생존율(1-J)를 곱함으로 얻을 수 있다. 출방할 때의 사망률은 각 J_w=0.3, J_d=0.17로 하였다(Wilkinson and Smith, 2002). Fuchs and Langenbach (1989)는 꿀벌응애가 약 2회 이내의 소방 침입을 하는 것으로 보고한 바있다.

소방으로 침입하는 꿀벌응애의 수(I)는 침입율이며 지수함수를 적용하였다. 수벌방 침입율($$ i_{d, t}=51.92\frac{D_t}{A_t}$$)은 일벌방 침입율 ($$ i_{w, t}=4.48\frac{W_t}{A_t}$$)보다 약 11배 크다(Boot et al., 1994; Boot et al., 1995; Calis et al., 1999). 이 때 일벌방으로 침입하는 꿀벌응애의 수($$ I_{w, t}=\frac{I_t{i}_{w, t}}{i_{w, t}+i_{d, t}}$$)이다. 만약, 꿀벌응애 암성충의 침입이 임의로 이루어진다고 가정하면, 일벌 애벌레방으로 침입한 평균 응애의수는 $$ {\theta }_{w, t}=\frac{I_{w, t}}{W_t}$$이고 수벌 애벌레방으로 침입한 평균응애의 수는 $$ {\theta }_{d, t}=\frac{I_{d, t}}{D_t}$$가 된다.

번식수(R_w,t , R_d,t)는 소방 당 침입한 암컷 응애 수에 따른 포아송 분포를 한다. 각 소방에서의 번식률은 λw=1.06, λd=2.44 이며 γ는 다수 응애의 침입했을 때 번식률 계수이다. 즉 한 마리의 꿀벌응애가 소방으로 침입할 경우 번식률 계수는 1이며, 여러 마리가 한 소방으로 들어갔을 때 그 계수는 작아진다. γw=0.84, 0.65, 0.6, 0.0이며 γd=0.91, 0.86, 0.60, 0.0으로 하였다(Martin, 1994; 1995a,b; Lobb and Martin, 1997; Martin and Kemp, 1997). 편승 중인 꿀벌응애의 사망수(G)는 당일 꿀벌응애의 수에 자연사망계수(m)를 곱하여 구한다. 자연사망계수는 여름철 0.016, 겨울철 0.003으로 하였다(Wilkinson and Smith, 2002; Kim and Jung, 2008).

결과 및 고찰

미래 기후 조건의 꿀벌 개체군에 미치는 영향

기상 요소의 변화는 꿀벌 생리대사는 물론 개체군 동태에 영향을 미칠 수 있다(Table 1). 그 중 온도의 변화가 꿀벌응애 개체군에 미치는 영향은 긍정적일 수 있다. 이는 꿀벌활동기간이 빨라지고 또 늦게까지 유지되면서 나타나게 된다. Table 1에서 보면 식물성장 기간은 230~322일에서 252~344일로 106~109% 증가할 것으로 전망되었다. 그런데 꿀벌활동은 일평균온도가 12°C 이상인 날로 잡을 수 있으며(Seeley, 1995), 이 기간은 현재 197~200일 정도 나타나는 데 향후 50년 내로 214~249일로 증가할 것으로 예측되었다. 따라서 빠르면3월 초순부터 꿀벌이 자유롭게 야외 활동을 하게 되고 가을철에는 11월 초순까지 활동을 하게 된다는 점이다. 따라서 꿀벌의 활동기간이 늘어나면서 꿀벌에게 먹이 등 자원공급이 제한되지 않는다면 꿀벌개체군 크기 및 분봉을 통한 번식은 더 왕성해질 수 있다. 우리나라의 경우 5월초 대규모 집중 유밀기에 대한(삭제) 대비하여 여왕벌의 산란개시는 빨라지고, 개체군 증식에 필요한 시간은 더 많아진다. 그러나 식물의 기후변화에 대한 적응 속도가 꿀벌 등 동물의 적응 속도와 같지 않을 가능성이 높다는 견해가 지배적이다(Visser and Both, 2005; Both et al., 2009). 식물이 반응속도가 늦어질 경우 꿀벌활동개시 시기와 초봄 식물 개화시기의 불일치는 단기적으로는 초봄의 꿀벌 춘감현상을 강화할 소지가 있고, 장기적으로는 초봄 번식이 늦은 꿀벌 집단의 선택이 지속될 수 있다. 즉 현재의 꿀벌 육종 체계의 변화가 생길 수 있다. 또한 봄철 빠른 산란으로 인해 비대해진 봉군은 여름철 무밀기에 급격한 저장식량 소비를 통해 봉군이 괴멸할 가능성도 생긴다(Le Conte and Navajas, 2008). 반면 그 외의 이상기후 특징들은 대부분 꿀벌 개체군 증식에 부정적 영향을 준다(Table 1). 우리나라 밀원식물의 주요 개화시기는 봄과 가을에 집중되어 있으며 여름철은 무밀기에 해당된다. 따라서 여름일수의 증가는 꿀벌에게 무밀기간의 확대로, 그리고 강우량의 증가와 호우일수의 증가는 먹이활동을 방해할 뿐 아니라 봉군 과밀과 과습 요건이 발생에 따른 봉군 내 저장먹이의 손실은 물론 질병에 노출 위험이 커질 수 있다. 또한 여름철 폭염과 열대야 일수의 증가는 봉군 내부 온도 유지를 위한 급수, 선풍, 피난 등의 추가적 에너지 소비가 요구될 뿐 아니라, 벌통 밖으로의 피난은 양서파충류는 물론 조류, 포유류 등 포식자들에 노출 위험이 커 질 수 있다. 반면 짧아진 겨울은 꿀벌의 월동 성공률을 높여줄 수 있으며 먹이소모량을 줄여 줄 수 있다. 반면 짧아진 결빙일수나 서리일수(Table 1)로 표현되는 온화해진 겨울은 꿀벌의 봉구 형성을 통한 대사열 발생의 지속성을 약화시키고, 간헐적 봉구의 해체는 꿀벌 개체의 저체온증으로 인한 낙봉 현상을 증가시킬 수 있다. 전반적으로 미래 기후 조건에서 꿀벌의 활동기간이 늘어나고 꿀벌 개체군 크기가 증가한다. 즉 꿀벌이 소모하는 자원의 양은 현재 규모보다 훨씬 커 질 것으로 판단되며, 특히 애벌레 양육을 위한 단백질 자원 획득 여부가 꿀벌 개체군 증가의 일차적 제한요소가 될 것으로 파악된다(Le Conte and Navajas, 2008). Table 2에서 제시된 꿀벌일벌 수의 변화는 여왕벌의 산락력에 직접 영향을 받으며, 산란수는 50일 즉 2월 초에 시작해서 4월말까지 지속적으로 증가하다가 그 이후는 산란수의 정체가 생긴다. 이 시기는 여름철로 밀원공급이 어렵고 또한 무더위, 강우 등 기상 상태가 불안정한 시기이기도 하다. 이후 가을철에 서서히 산란수는 줄어들면서 11월 초 월동 준비로 들어간다. 꿀벌 개체수는 산란수 패턴보다 약 21일 정도 늦게 나타난다(Fig. 3).

Fig. 3.

Hypothetical population dynamics of honeybee eggs (broken line) and adult workers, At (solid line) based on the daily oviposition, et (dotted line).

미래 기후 조건에서 꿀벌응애 개체군 변동

꿀벌 응애의 개체군 변화는 현재의 기후 조건과 미래의 기후 조건에서 시뮬레이션을 하였다. 무관리 상태에서 꿀벌응애 연중 개체군 밀도 변동에 월동 후 초기밀도의 영향은 매우 크다(Jung, 2012). 그러나 국내에서 꿀벌응애 관리는 봄철 꿀벌 증식을 시작하면서 약제 처리를 하기 때문에(Kim and Jung, 2008), 월동밀도에 상관 없이 초기 꿀벌응애 밀도는 비슷하게 된다. 따라서 본 연구에서는 월동 초기 개체군 암컷 성충밀도가 봉군 당 10마리로 가정하고 두 가지 기후조건에 대한 시뮬레이션을 실시한 결과는 Fig. 4와 같다. 현재 기후와 미래 기후 조건에서 살비제를 처리하지 않았을 경우 월동 전 꿀벌응애의 봉군 당 밀도는 7.7천 마리와 10.4천 마리로 나타났다. 즉 꿀벌응애의 밀도는 현재보다 약 35% 증가할 것으로 예측되었다. 꿀벌응애의 통상적 방제밀도는 일벌의 5% 내외가 감염되었을 때를 잡으며, 그 밀도가 일벌의 10% 이상이 되면 봉군은 사멸하기 시작한다(Jung and Kim, 2008). 통상적으로 여름철 봉군 규모를 3만 마리 정도를 유지한다면(Seeley, 1995). 꿀벌응애 방제밀도는 1500여마리가 될 것이며, 월동시기에는 그 보다 훨씬 더 낮은 수준이어야 한다. 이에 따라 봄과 여름에 임계밀도가 되었을 때 두 번의 약제 방제를 한 후에 꿀벌응애 밀도는 각각 78과 654마리로 나타났다. 미래 기후 조건에서 약제 처리 후 후기 꿀벌응애 밀도는 10배 이상 높게 예측되었다. 이 경우 봉군 당 78마리는 추가적 방제를 하지 않아도 월동 기간 중 자연낙마(G=0.003)를 통해 밀도가 감소된다. 반면 654마리 봉군은 반드시 추가적 방제를 통해서 밀도를 억제해야 월동에 성공할 수 있다(Seeley, 1995).

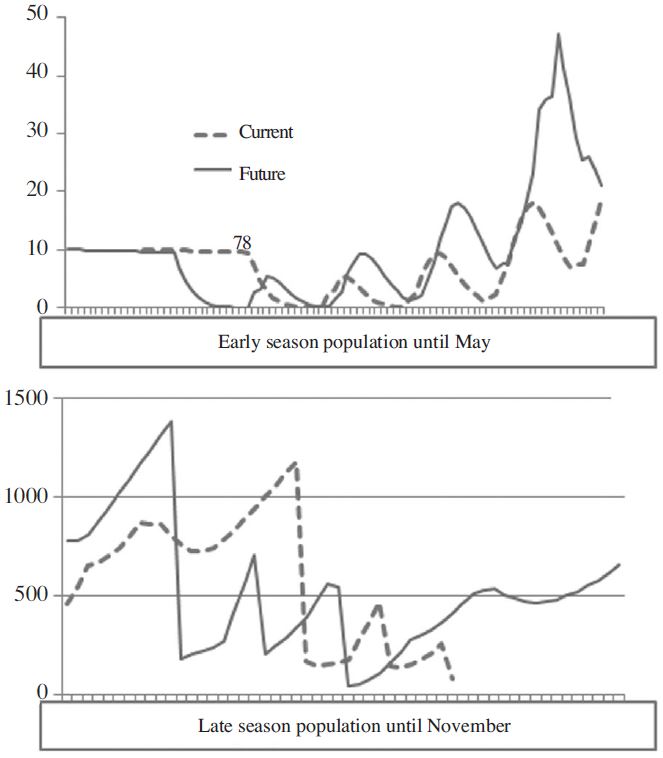
Fig. 5는 두 기후 조건에서 봄철과 가을철의 꿀벌응애 밀도 전개 패턴을 비교하였다. 봄철 꿀벌응애 밀도는 월동 개체군에서 시작된다. 꿀벌응애는 월동봉구를 형성하는 꿀벌의 날개죽지 등 보호되는 장소에 부착하여 겨울을 보낸다. 월동 중 꿀벌의 사망률은 0,01수준이며, 꿀벌응애의 사망률은 0,003으로 알려졌다(Wilkinson and Smith, 2002). 꿀벌응애의 겨울철 사망률은 전적으로 바닥에 떨어져서 죽는 개체의 비율을 산정한 것으로 추후 국내 환경에 맞는 파라미터의 추정이 필요하다. 따라서 월동 중 꿀벌응애의 밀도는 점차 감소하나, 봄철에 꿀벌 육아가 진행되면 꿀벌응애는 번식을 위해 꿀벌 애벌레 소방으로 거의 침입한다(Beetsma et al., 1999). 그 후 편승 꿀벌응애의 밀도는 산란 주기에 맞추어 등락을 반복하면서 지속적으로 증가한다(Fig. 4. upper graph). 그러나 전술한 바와 같이 초기 살비제를 통한 방제가 이루어지기 때문에(Kim and Jung, 2008), 약효가 일정하다고 가정하면 시작 밀도는 매우 낮고 벌통마다 균일하게 된다. 이 경우, 미래 기후 조건에서는 꿀벌활동기간이 크게 앞당겨지기 때문에, 꿀벌의 산란과 육아, 그리고 꿀벌응애의 번식은 한 주기 정도 먼저 시작된다. 그럼에도 불구하고 5월 말까지 개체군 밀도는 군당 100마리 이하에서 유지됨을 볼 수 있다. 즉, 봄철에는 초기 밀도 억제가 이루어 졌을 경우, 유밀기인 5월까지는 꿀벌응애의 피해로부터 비교적 안전하다는 것을 보여준다. 물론 약제 선택에 따라 다른 밀도로 시작하는 경우도 상정할 수 있다. 그 효과는 이미 Jung(2012)에서 검토되었다.

반면, 방제 밀도를 조금 낮게 설정하여 3회 처리 후 가을철 남아있는 꿀벌응애 개체군 크기를 비교한 Fig. 5(lower graph)의 경우, 9월 약제 처리가 부족할 수 있음을 보여준다. 미래 기후 조건에서 꿀벌응애 밀도는 초가을 1,400마리에 이르기 때문에 1주일 간격으로 3회 연속 약제를 처리한 결과, 그 밀도는 20 내외로 낮아졌다. 그러나 미래 기후 조건에서는 9월말과 10월까지도 일부 꿀벌의 산란과 육아가 진행되기 때문에 꿀벌응애 역시 번식이 빠르다. 11월에 접어들면서 꿀벌응애 밀도는 다시 600여 마리 수준으로 회복된다. 반면 현재 기후 조건에서는 9월 말 1회의 방제로 꿀벌응애 밀도는 관리가 가능하다.

이상을 종합해 보면, 미래 기후 환경에서 꿀벌의 개체군 크기는 증가할 수 있으나 다양한 밀도 억제 또는 밀도 억제 요인이 존재함을 알 수 있다. 꿀벌응애는 초봄 빠른 번식 기회를 활용하여 개체군 크기는 전반적으로 35% 내외로 더 커질 것으로 예측되었다. 또한 밀도 억제를 위한 효과적인 방법으로 개선되어야 함을 지적하고 있다. 현재의 약제 방제 체계로는 미래 기후에서는 3회의 살비제 처리로는 월동 전 꿀벌응애 밀도를 안정적으로 억제하기 어렵다는 점을 시뮬레이션 결과는 보여주고 있다. 이는 꿀벌응애의 높은 개체군 증가율과도 연관되어 있다. Wilkinson and Smith(2002)는 안정 개제군의 내적자연증가율이 0.0139, 그리고 Martin(1998)과 Calis et al.(1999)는 개체군 증가율이 0.02 수준으로 보고하였다. 그러나 수벌 방 등 유충 소방이 충분하고 개체군 밀도가 증가하는 시기에 개체군 증가율은 모델 시뮬레이션에서는 0.031~0.046로 추정되었고(Jung, 2012), 실제 경북 안동 소재 실험양봉장에서 추정한 값은 0.08이었다. 꿀벌응애 개체군은 다양한 가정과 가설에 기반한 모델 예측보다 훨씬 더 빠른 속도로 증식할 수도 있음을 시사한다. 향후 수벌방 제거나 여왕 격리를 통한 산란 억제 등의 단독 처리 또는 약제 살포 등과의 교호 처리 등 꿀벌응애류 종합관리를 위한 다양한 전략에 대한 시뮬레이션 연구가 필요할 것으로 보인다. 또한 이 모형에는 다양한 가정과 파라미터들이 제시되었는 데 각각에 대한 민감도 분석을 통한 최적관리 방안 개발도 요구된다(Drechsler, 1998). 최근 우리나라에서도 꿀벌의 남방계 해충인 가시응애의 피해가 증가하는 경향이 있다(Choi et al., 2014). 태국 등 동남아지역에서는 가시응애에 비하여 꿀벌응애의 밀도가 상대적으로 매우 낮다(Kavinseksan et al., 2003). 따라서 우리나라가 점점 아열대기후로 변해가는 와중에, 양봉꿀벌에서는 꿀벌응애외 가시응애의 조우, 공존 또는 경쟁이 일어날 수 있으며, 이는 꿀벌응애 개체군 동태에 영향을 줄 수 있기에 주의깊은 관찰을 통한 밀도 변동 모니터링이 필요하다.

Fig. 4.

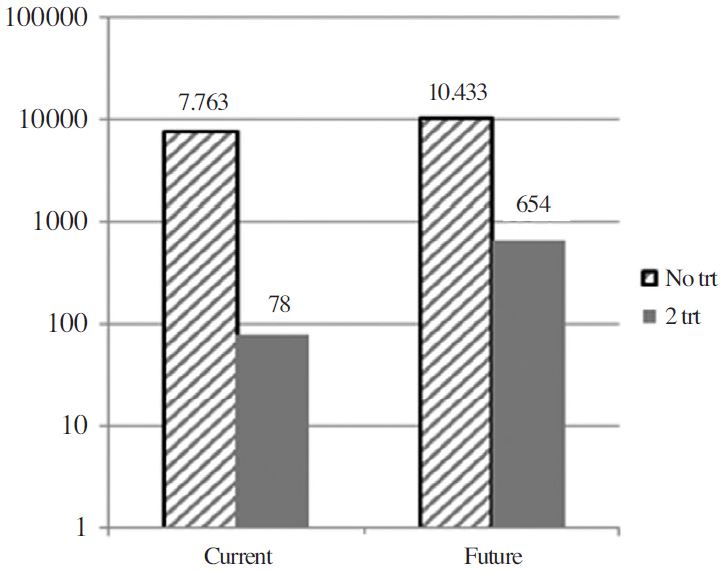
End season population size of varroa mites (number per colony) simulated under current and future climatic conditions. Slashed bars were from no treatment colonies and filled bars from two time acaricide treatment colonies. Number on the bar is the mite density.

Fig. 5.

Simulated population behavior of varroa mites under current and future climatic conditions of early season (upper) and late season (lower). Dotted line for current pattern and solid line for future pattern.

적 요

꿀벌응애는 꿀벌 건강을 위협하는 가장 중요한 외부기생성 해충으로, 동양종꿀벌에서 양봉꿀벌로 기주이동을 한 이래, 지속적으로 그 중요성이 높아져 가고 있다. 특히 최근의 기후변화는 꿀벌응애의 심각성에 강화하고 있는 것으로 파악되는 바, 기상청의 미래 기후 자료를 분석하고 그를 이용하여 꿀벌응애 개체군 동태를 모의 연구하였다. 미래 기후 조건은 꿀벌의 활동기간 및 개체군 크기에는 긍정적 영향을 미치지만, 여름철과 겨울철의 이상 기후 현상들은 부정적 영향을 미치는 것으로 파악되었다. 꿀벌응애의 개체군 크기는 미래 기상 조건에서 약 35% 증가하는 것으로 나타났다. 보수적 기준으로 2회 방제 후 가을철 밀도를 비교해 봤을 때 현재 기후조건에 비해 미래 기후조건에서 약 10배 이상의 개체군 크기를 보였다. 꿀벌 밀도 대비 5% 방제수준에서 3회 방제한 후 가을철 꿀벌응애 밀도는 역시 추가 방제를 요구하는 수준이었다. 즉, 미래 기후 조건에서 꿀벌응애의 영향은 더욱커질 것으로 예측되었고, 현재의 약제 방제 이외의 밀도 억제 기작 연구가 필요함을 시사한다.

Acknowledgments

본 연구는 농림부 농림기술관리센터 Bio Industry Technolog Development Program(Nr. 312027-3)의 지원을 받았습니다. 또한 농림부지원 지역곤충자원산업화센터 R&D센터의 기자재를 활용하였습니다.

Reference

• 기상청, (2012), 한반도 기후변화 전망 보고서, p151, 기상청.
• 우건석, 이종호, (1993), 우리나라 꿀벌과 벌통에서 서식하는 응애류에 관한 연구I, 한양봉지, 8, p140-156.
• 우건석, 조광선, 류영수, (1994), 꿀벌에 기생하는 응애에 의한 피해 실태 조사 분석, 한양봉지, 9, p33-39.
• 이명렬, 이만영, 김영수, 남성희, 장승종, 유철형, (2004), 꿀벌응애 약제 및 몇 가지 천연물의 꿀벌응애 방제 효과에 대한 예비평가, 한양봉지, 19, p57-60.
• 정진교, 이만영, 마영일, (2000), 1999 2000년 국내서 서양종꿀벌(Apis mellifera L.) 양봉농가에서 꿀벌응애와 중국 가시응애의 감염 실태 조사, 한양봉지, 15, p141-145.
• 최승윤, 우건석, 김영수, (1986), 꿀벌응애에 관한 설문 조사 및 분석, 한양봉지, 1, p62-75.
• 최용수, 이명렬, 이만영, (2007), 국내꿀벌에서Israel Acute Paralysis Virus (IAPV) 진단, 한양봉지, 22, p159-165.
• Allen, M. D., (1963), Drone production in honey bee colonies (Apis mellifera L.), Nature, 199, p780-790. [https://doi.org/10.1038/199789a0]
• Allen, M. D., (1965), The effect of a plentiful supply of drone comb on colonies of honeybees, J. Apicult. Res, 4, p109-119.
• Anderson, D. L., and J. W. Trueman, (2000), Varroa jacobsoni(Acari: Varroidae) is more than one species, Exp. Appl. Acarol, 24, p165-189. [https://doi.org/10.1023/A:1006456720416]
• Andrew, N. R., S. J. Hill, M. Binns, M. H. Bahar, E. V. Ridley, M. Jung, C. Fyfe, M. Yates, and M. Khusro, (2013), Assessing insect responses to climate change: What are we testing for? Where should we be heading?, PeerJ, 1, e11. [https://doi.org/10.7717/peerj.11]
• Beetsma, J., W. J. Boot, and J. Calis, (1999), Invasion behaviour of Varroa jacobsoni Oud.: from bees into brood cells, Apidologie, 30, p125-140. [https://doi.org/10.1051/apido:19990204]
• Boecking, O., and W. Ritter, (1994), Current status of behavioural tolerance of the honeybee Apis mellifera to the mite Varroa jacobsoni, Am. Bee J., 134, p689-694.
• Boot, W. J., J. Schoenmaker, J. N. M. Calis, and J. Beetsma, (1995), Invasion of Varroa jacobsoni into drone brood cells of the honey bee, Apis mellifera, Apidologie, 26, p109-118. [https://doi.org/10.1051/apido:19950204]
• Boot, W. J., D. J. A. Sisselaar, J. N. M. Calis, and J. Beetsma, (1994), Factors affecting invasion of Varroa jacobsoni (Acari: Varroidae) into honeybee, Apis mellifera (Hymenoptera: Apidae), brood cells, Bull. Entomol. Res, 84, p3-10. [https://doi.org/10.1017/s0007485300032168]
• Both, C., M. van Asch, R. G. Bijlsma, A. B. van den Burg, and M. E. Visser, (2009), Climate change and unequal phenological changes across four trophic levels: Constraints or adaptations?, Journal of Animal Ecology, 78, p73-83. [https://doi.org/10.1111/j.1365-2656.2008.01458.x]
• Calis, J. N. M., I. Fries, and S. C. Ryrie, (1999), Population modelling of Varroa jacobsoni Oud, Apidologie, 30, p111-124. [https://doi.org/10.1051/apido:19990203]
• Choi, S. Y., K. S. Woo, and Y. S. Kim, (1986), Questionary survey on the varroa mites in Korean beekeeping, Kor. J. Apic, 1, p62-75.
• Choi, Y. S., M. L. Lee, H. S. Sim, H. K. Kim, K. H. Byeon, M. Y. Yoon, A. R. Kang, T. V. Toan, I. P. Hong, and S. O. Woo, (2014), Molphological Analysis and Determination of Interference Competition between Two Honeybee Mites: Varroa destructor and Tropilaelaps clareae (Acari: Varroidae and Laelapidae), Kor. J. Apic, 29, p327-332. [https://doi.org/10.17519/apiculture.2014.11.29.4.327]
• Cox Foster, D., and D. van Engelsdorf, (2009), Saving the honeybee, Scientific America, March p40-47. [https://doi.org/10.1038/scientificamerican0409-40]
• Drechsler, M., (1998), Sensitivity analysis of complex models, Biol. Conserv, 86, p401-412. [https://doi.org/10.1016/S0006-3207(98)00021-4]
• Fries, I., S. Camazine, and J. Sneyd, (1994), Population dynamics of Varroa jacobsoni: a model and a review, Bee World., 75, p5-28. [https://doi.org/10.1080/0005772X.1994.11099190]
• Fuchs, S., and K. Langenbach, (1989), Multiple infestation of Apis mellifera L. brood cells and reproduction in Varroa jacobsoni Oud, Apidologie, 20, p257-266. [https://doi.org/10.1051/apido:19890308]
• IPCC, (2007), Summary for Policymakers, In: Climate Change 2007, The Physical Science Basis, Contribution of Working Group l to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change Solomon, S., D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt, M. Tignor, and H. L. Miller eds, Cambridge University Press, United Kingdom and USA.
• Jung, C., (2009), Frame work of the adaptive population model of varroa mite in Korean beekeeping environment, Kor. J. Apic, 24, p67-74.
• Jung, C., (2012), Incorporation of damage function of varroa mites into Honeybee varroa mite interaction model, Kor. J. Apic, 27, p67-74.
• Jung, C., and D. Kim, (2008), A population model of varroa mite, Varroa destructor in adult honey bees in the colony. I. Exponential population growth, Kor. J. Apic, 23, p269-273.
• Jung, J. K., M. Y. Lee, and Y. I. Mah, (2000), Infestation of Varroa jacobsoni and Tropilaelaps clareae in some apriaries during spring and fall seasons, 1999 2000 in South Korea, Kor. J. Apic, 15, p141-145.
• Kavinseksan, B., S. Wongsiri, L. I. de Guzman, and T. E. Rinderer, (2003), Absence of Tropilaelaps infestation from recent swarms of Apis dorsata in Thailand, J. Apic. Res, 42, p49-50.
• Kim, D., and C. Jung, (2008), Evaluation of chemical susceptibility of the ectoparasitic mite Varroa destructor in honey bee (Apis mellifera L.), Kor. J. Apic, 23, p261-268.
• Korpela, S., A. Aarhus, I. Fries, and H. Hansen, (1992), Varroa jacobsoni Oud. in cold climates: population growth, winter mortality and influence on the survival of honey bee colonies, J. Apicult. Res, 31, p157-164.
• Kraus, B., and R. E. Page, (1995), Population growth of Varroa jacobsoni Oud. in Mediterranean climates of California, Apidologie, 26, p149-157. [https://doi.org/10.1051/apido:19950208]
• Le Conte, Y., M. Ellis, and W. Ritter, (2010), Varroa mites and honey bee health: can Varroa explain part of the colony losses?, Apidologie, 41, p353-363. [https://doi.org/10.1051/apido/2010017]
• Le Conte, Y., and M. Navajas, (2008), Climate change: Impact on honeybee populations and diseases, Rev. Sci. Off. int. Epiz, 27, p499-510.
• Lobb, N., and S. Martin, (1997), Mortality of Varroa jacobsoni Oudemans during or soon after the emergence of worker and drone honeybees Apis mellifera L., Apidologie, 28, p367-374. [https://doi.org/10.1051/apido:19970604]
• Martin, S., (1998), A population model for the ectoparasitic mite Varroa jacobsoni in honey bee (Apis mellifera) colonies, Eco. Model, 109, p2677-281. [https://doi.org/10.1016/S0304-3800(98)00059-3]
• Martin, S. J., (1994), Ontogenesis of the mite Varroa jacobsoni Oud. in worker brood of the honeybee Apis mellifera L. under natural conditions, Exp. Appl. Acarol, 18, p87-100. [https://doi.org/10.1007/BF00055033]
• Martin, S. J., (1995a), Ontogenesis of the mite Varroa jacobsoni Oud. in drone brood of the honeybee Apis mellifera L. under natural conditions, Exp. Appl. Acarol, 19, p199-210. [https://doi.org/10.1007/BF00130823]
• Martin, S. J., (1995b), Reproduction of Varroa jacobsoni in cells of Apis mellifera containing one or more mother mites and the distribution of these cells, J. Apicult. Res, 34, p187-196.
• Martin, S. J., and D. Kemp, (1997), Average number of reproductive cycles performed by Varroa jacbsoni in honey bee (Apis mellifera) colonies, J. Apicult. Res, 36, p113-123.
• Neukirch, A., (1982), Dependence of the life span of the honeybee (Apis mellifera) upon flight performance and energy consumption, J. Comp. Physiol. B, 146, p35-40. [https://doi.org/10.1007/BF00688714]
• Oldroyd, B. P., (1999), Coevolution while you wait: Varroa jacobsoni, a new parasite of western honeybees, Trends Ecol. Evol, 14, p312-315. [https://doi.org/10.1016/s0169-5347(99)01613-4]
• Peng, Y. S., Y. Fang, S. Xu, and L. Ge, (1987), The resistance Mecanism of the Asian Honey Bee, Apis cerana Fabr., to an Ectoparasitic Mite, Varroa jacobsoni Oudemans, J. Invertebr. Pathol, 49, p54-60. [https://doi.org/10.1016/0022-2011(87)90125-X]
• Sammataro, D., U. Gerson, and G. Needham, (2000), Parasitic mites of honey bees: Life history, implications and impact, Annu. Rev. Entomol, 45, p519-548. [https://doi.org/10.1146/annurev.ento.45.1.519]
• Seeley, T. D., (1985), Temperature control, p107-122, in Honeybee ecology: Astudy of adaptation in social life, p201Princetion University Press, New Jersey.
• Visser, M. E., and C. Both, (2005), Shifts in phenology due to global climate change: the need for a yardstick, Proceedings of the Royal Society of London Series B Biological Sciences, 272, p2561-2569. [https://doi.org/10.1098/rspb.2005.3356]
• Watanabe, M. E., (2008), Colony Collapse Disorder: Many suspects, no smoking gun, BioScience, 58, p384-388. [https://doi.org/10.1641/B580503]
• Wilkinson, D., and G. C. Smith, (2002), A model of the mite parasite, Varroa destructor, on honeybees (Apis mellifera) to investigate parameters important to mite population growth, Ecol. Model, 148, p263-275. [https://doi.org/10.1016/S0304-3800(01)00440-9]
• Woo, K. S., and J. H. Lee, (1993), The study on the mites inhabiting the bee hives in Korea, Kor. J. Apic, 8, p140-156.